Система Mathematica пытается решить алгебраическое уравнение пятой степени

Пример 1.8 . Система Mathematica пытается решить алгебраическое уравнение пятой степени

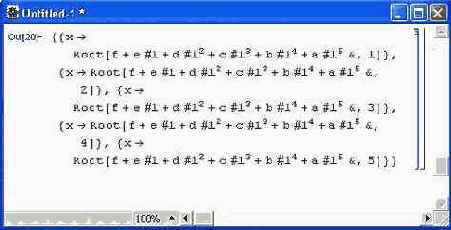
А вот и сюрприз: Mathematica не только не отказалась решать эту задачу (при отказе она просто повторяет вводимое выражение), но даже подсказала путь ее решения с помощью пятикратного применения функции вычисления корней Root степенных многочленов.

В упомянутых примерах мы сталкиваемся с одной из серьезных проблем символьной математики — разбуханием результатов аналитических преобразований при порой незначительном усложнении решаемых задач. В данном случае это никоим образом не является недостатком систем компьютерной математики как таковых — просто так нарастает сложность решения данной математической задачи в соответствии с канонами абстрактной математики.

Однако нередко разбухание результатов кроется в сложности алгоритмов, особенно рекурсивных. Современные системы символьной математики способны осуществлять весьма глубокую рекурсию, и порой трудно даже предположить, к сколь громоздкому результату это в конечном счете приведет.

Научные работники и инженеры настолько привыкли к упрощению (порой весьма грубому, с точки зрения математиков), что громоздкие решения, получаемые с помощью систем символьной математики, способны их раздражать. Это в определенной мере препятствует применению систем символьной математики на практике и в наши дни.

Однако для частных случаев нередко можно получить вполне сносные по виду решения. Вот пример решения неполного алгебраического уравнения десятой степени, при котором Mathematica благополучно возвращает все десять корней довольно простого вида (рис. 1.9 ).

Примеры такого рода можно встретить повсеместно. Есть множество нелинейных алгебраических или дифференциальных уравнений обманчиво простого вида, но имеющих сложнейшие решения или не имеющих их вовсе. Так что если система символьной математики не находит ответ, это зачастую не является признаком ее слабости — может быть, решения не существует вообще? Порой даже такой отрицательный результат избавляет пользователя от трудоемкого поиска несуществующих решений «в лоб» и направляет его на поиск обходных, порою весьма ценных и полезных методов решения.