Примеры вычислений из области математического

Пример 1.


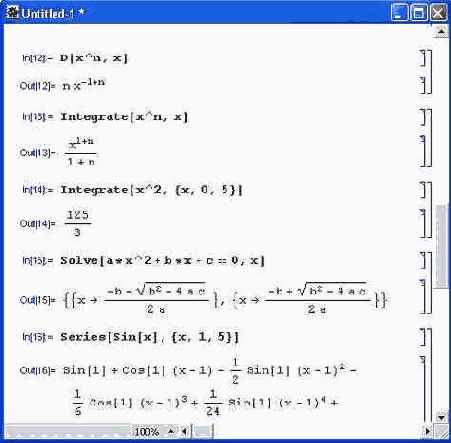
6 . Примеры вычислений из области математического анализа
В этих примерах функция D (как приятное исключение из правил, обозначенная одной буквой) вычисляет производную, функция Integrate — интеграл, функция Solve решает нелинейное уравнение (в данном случае квадратное), а функция Series разлагает выражение в ряд относительно заданной переменной и при заданных начальном значении переменной и максимальной степени ряда. В фигурных скобках задаются списки некоторых входных и выходных параметров (аргументов).
Системы символьной математики являются справочниками по многим специальным функциям. При этом они способны давать результаты вычислений в виде специальных функций, что демонстрируют следующие примеры:
Sum[1/k^9,{k,1,n}]
HarmonicNumber [n, 9]
Integrate [Log [x] *Exp [ -х^4 ], {x, 0, Infinity}]
-1/32*Gamma[ 1/4 ] ( 2 EulerGamma + л + Log[64] )
DSolve[y " [t] + y' [t] + y[t]/t = 0, y[t] , t]
{{y[t]->e^-tC[1]+e^-tC[2]Gamma[-1,-t]}}
Здесь специальные функции получаются в результате вычисления суммы, символьного интегрирования и решения в аналитическом виде дифференциального уравнения. Соответствующие функции будут более подробно описаны в дальнейшем. Обратите внимание на то, что эти примеры даны прямо в тексте книги. Мы будем часто использовать такой прием для представления небольших примеров.

Чем дальше в лес, тем больше дров!
К сожалению, в математике нередко оказывается так, что результирующие выражения быстро нарастают по сложности при, казалось бы, незначительном усложнении или просто изменении условий задачи. Покажем это на примере решения одной из самых часто встречающихся задач — поиска в аналитическом виде корней алгебраического уравнения с целыми степенями членов.
Многие из нас прекрасно помнят формулы для корней квадратного уравнения, которые нам давали еще в школе. Их в точности воспроизвела Mathematica в одном из примеров, приведенных в этом уроке чуть ранее. Это решение еще раз воспроизведено на рис. 1.7 (сверху).